Frequentist Statistics 3

In my past post, I talked a lot about the normal distribution and how to check if your data has normality. One of the reasons we rely on a normal distribution is because of the null distribution, the sampling distribution under the null hypothesis. Basically, how many observations you have, the size of your n, determines how your null distribution looks. In the next post I’ll talk more how this relates to significance testing.

The Null Hypothesis

The null hypothesis, H0 as it’s often referred as, can often be viewed as that there is no difference between two groups. For example if we have two groups, G1 and G2, and we think G1 is taller than G2, the H0 is, $G1 height = G2 height$. If we add a third group, G3, H0 becomes $G1 height = G2 height = G3 height$. When the = sign is used here, it doesn’t mean literally equal to each other, it mean statistically equal to each other and we use the null distribution to help determine this.

The Alternative Hypothesis

The alternative hypothesis, H1 as it’s often referred as, can often be viewed as that there is a difference between two groups. Using the last example, H1 would be $G1 height \neq G2height$.

##Hypothesis Testing One-sided testing is when you only test one side for the null distribution.

# draw the normal curve
curve(dnorm(x,0,1), xlim=c(-3,3), main="Normal density")
 
# define shaded region
to.z = 3
from.z = qnorm(.95)
 
S.x  = c(from.z, seq(from.z, to.z, 0.01), to.z)
S.y  = c(0, dnorm(seq(from.z, to.z, 0.01)), 0)
polygon(S.x,S.y, col="red")

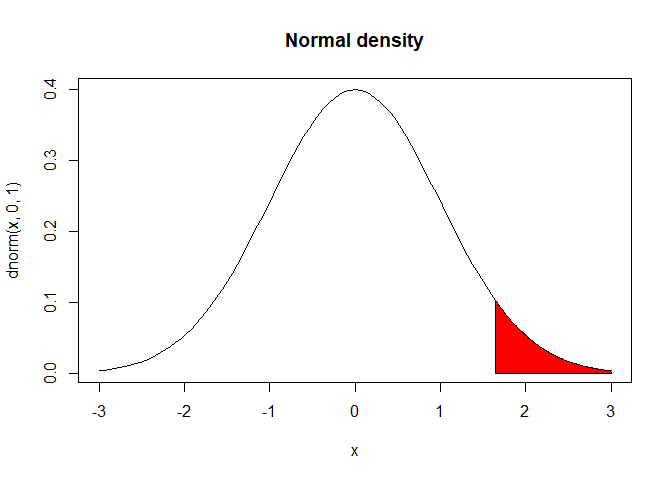
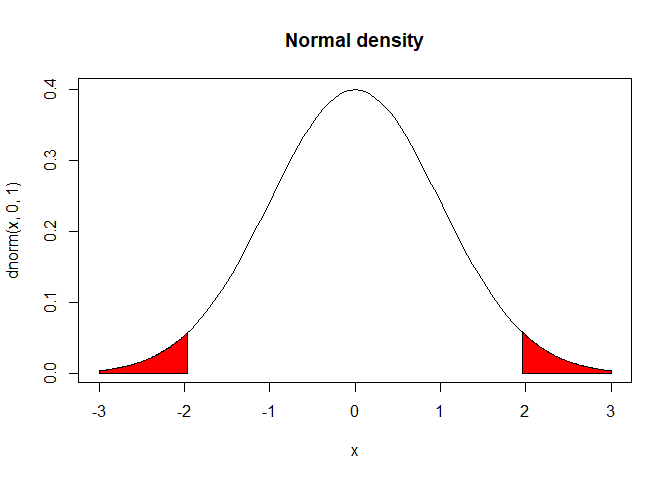
Two-sided testing is when you test both sides of the null distribution. This is when you have a non-directional hypothesis. For example, what if you don’t have any idea if G1 or G2 is taller but you do have an inkling that there is a difference between the two groups. This is when you’ll use a two-sided test.

# draw the normal curve
curve(dnorm(x,0,1), xlim=c(-3,3), main="Normal density")
 
# define shaded region
from.z1 = -3
to.z1 = qnorm(.025)
 
a.x  = c(from.z1, seq(from.z1, to.z1, 0.01), to.z1)
a.y  = c(0, dnorm(seq(from.z1, to.z1, 0.01)), 0)
polygon(a.x,a.y, col="red")

#define shaded region
to.z2 = 3
from.z2 = qnorm(.975)

b.x  = c(from.z2, seq(from.z2, to.z2, 0.01), to.z2)
b.y  = c(0, dnorm(seq(from.z2, to.z2, 0.01)), 0)
polygon(b.x,b.y, col="red")

Errors

1. Type I Error is when you have a false positive, when you find a significant difference ($G1 height \neq G2height$) when the truth is $G1 height = G2height$.

2. Type II Error is when you have a false negative, when don’t find a significant difference ($G1 height \neq G2height$) when the truth is $G1 height = G2height$.

Null hypothesis testing errors

	H0 True	H0 False
Reject H0	Type I Error	Correct
Accept H0	Correct	Type II Error

Now, telling if you have a type I or II error is much more tricky. There a lot of things you can do to help to not have one but you can never really can no. You also might be wondering if it’s better to have a type I or II error because some tests are more prone to one over the other. In neuroimaging, people generally prefer tests that are more prone to type I errors in lieu of type II errors because positive results are more publishable and are type I errors necessarily worse than type II errors? I don’t think I’m qualified to answer that and I’ll let you make your own judgments on it.

In the next post I’ll talk about how to test for statistical differences between two groups